FlareOn-9 Writeups 09 Encryptor

Introduction
Description:
You’re really crushing it to get this far. This is probably the end for you. Better luck next year!
Yay, looks like we’ll have some cryptography homework with this challenge !
The challenge consist of an x86_64 Windows binary and an encrypted file named SuspiciousFile.txt.Encrypted.
Of course, the encrypted file is not readable (for now):
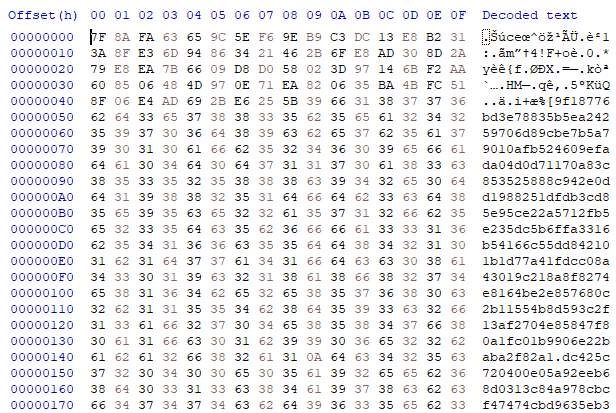
The binary seems to take a file as an argument, and is supposed to encrypt it:
#flareon.exe
usage: flareon path [path ...]
#flareon.exe test.txt
0 File(s) Encrypted
Time to understand how this works.
Analysis
After doing a bunch of initialization work that we can ignore for the moment, the program takes a provided file-path as argv[1], encrypt it (only an assumption for the moment), and write down the encrypted version on disk, with the .Encrypted extension:
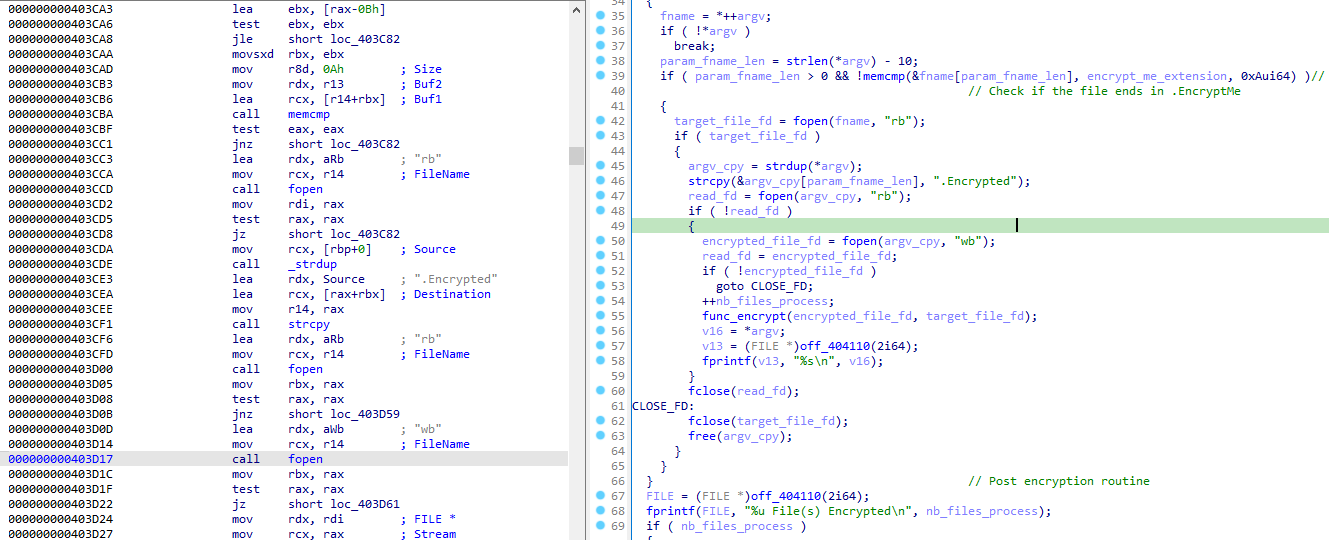
Our initial test wasn’t successful as the given file must have the .EncryptMe extension.
If we retry, this time we managed to generate an encrypted version of a random file:
#flareon.exe test.txt.EncryptMe
1 File(s) Encrypted
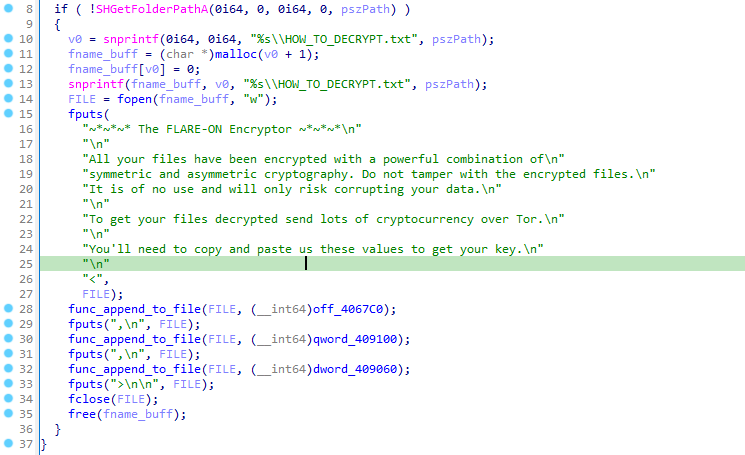
We can also spot that a file named HOW_TO_DECRYPT.txt is dropped on disk after the encryption of a file:
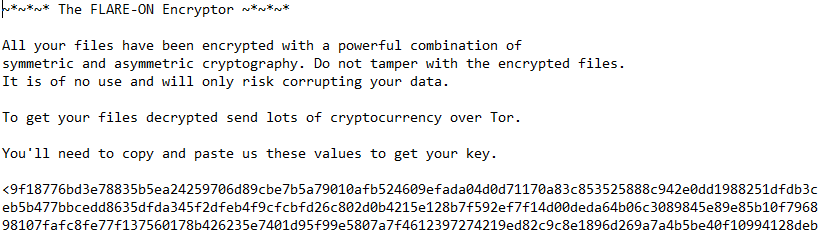
This looks like a pseudo-ransom note, funny :)
We don’t know for now, but 3 hexadecimal values are appended to the file:
These are probably some sort of important cryptographic values that should allow the decryption of the file. From our tests, only the first value is consistent across multiple encryption and the two remaining seems unique for each run.
The function in charge of the encryption process is only calling a few other functions, doing some manipulations on the file we want to encrypt:
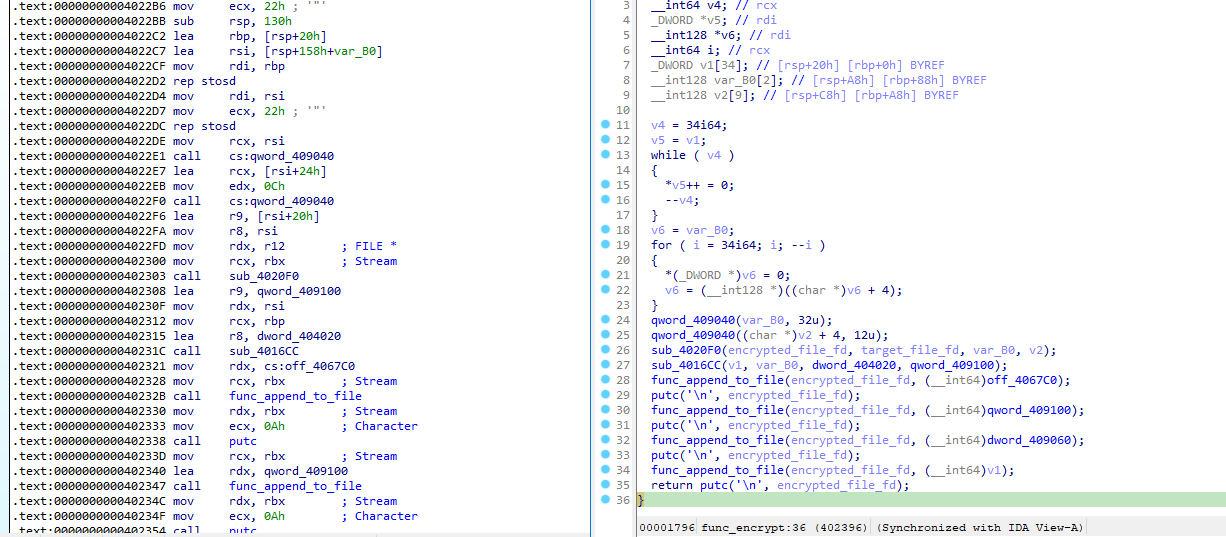
Before exploring them one-by-one, qword_409040 is the RtlGenrandom function. This function can be resolved by the alias SystemFunction036:

Let’s start by analyzing sub_4020F0.
xChaCha20 Algorithm
This first function act as a wrapper for the xChaCha20 algorithm, which is a variant of the Salsa20 algorithm.
Salsa20 / ChaCha20 / xChaCha20 is a symmetric stream-cipher algorithm. It is in fact one of the best competitor to AES.
ChaCha20 works by using an initial state of 512 bits, containing a “nothing up my sleeve” constant string (128 bits), a 256 bits key, a 64 bits counter and a 64 bits nonce.
The “nothing up my sleeve” value is the string expand 32-byte k by default, which can help us recognize the Salsa20 algorithm family:

The xChaCha variant can be spot as it uses a nonce of 96 bits (instead of the 64 bit long one).

The algorithm is using a PRGA to generate random values from the initial state, and these values are xored against the plaintext to perform the actual encryption / decryption:
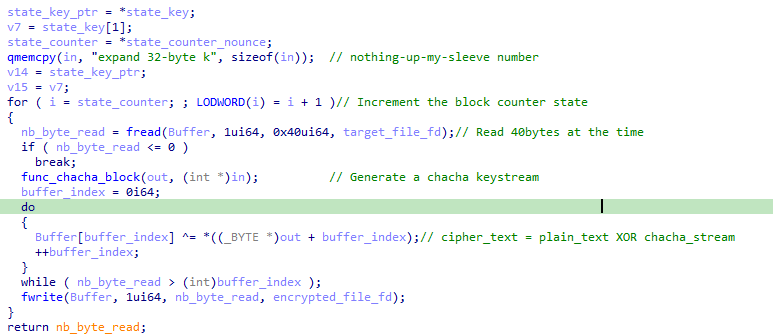
The xChaCha20 keystream is generated using a set of multiple XOR and rotation operations, which makes it resilient to most of the side-channel attacks that we can think of (on RSA for instance), as the time to compute the operations is always the same regarding on the provided input.
The initial state is represented as a 4x4 matrix, and each columns and diagonals of this matrix are manipulated in 20 consecutive rounds. This is where the diffusion of the initial plaintext key is happening.
By looking at the func_chacha_block function, we can retrieve the standard operations performed on each column / diagonal. For instance, here is are the operations performed on the 4th diagonal (the last one):

And here are the others xChaCha20 internal operations for the first 3 columns:

Taking a step back, we have the following information:
- A 256 bit xChaCha20 key is randomly generated using RtlGenrandom().
- A 96 bit xChaCha20 nonce is randomly generated using RtlGenrandom().
- The file content is encrypted using the random values.
But that’s not all, as something else is operating on the xChaCha20 key:
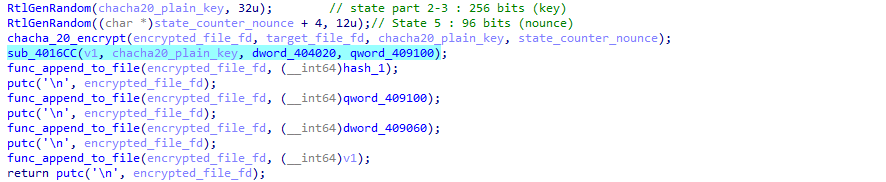
And it seems that the result of this last operation is appended at the end of the encrypted file + in the “ransom note”.
RSA Algorithm
I actually spent a few days reversing this last function before realizing what it is.
Spoiler alert: this is RSA encryption, but I missed the well-known default exponent value of RSA 65537 …

I guess I learned the hard way that 0x10001 equal 65537 :)
In this madness phase of reverse-engineering of an optimized RSA algorithm function, I even re-wrote my own version of it from the assembly:
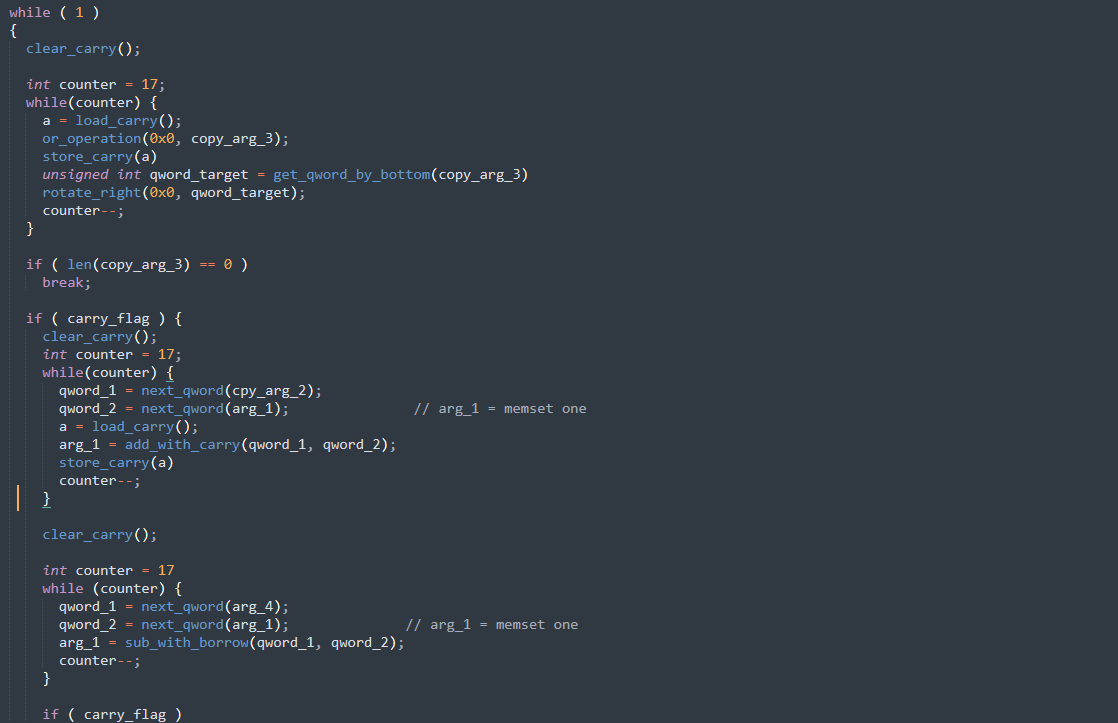
After some times I finally recognized the algorithm, but it still gives me some PTSD just to think about it. Anyway, let’s move on.
RSA is an asymmetric encryption algorithm that works with a set of private and public keys.
A public key is composed of the values (e,N).
e: the exponent.N: the modulus.
The modulus is a large random number obtained by the addition of two primes number (named p and q).
These two element are public by definition, and should be exposed.
Then, the private key d is calculated from ed ≡ 1 (mod(p-1)(q-1)).
And obviously, this value should be kept secret.
When the sender and the receiver have both generated a set of public / private key pair, the sender can use the receiver’s public key to encrypt its message. As the private key corresponding to this public key is only known by the receiver, the message can only be decrypted by the receiver.
Something important to note is that RSA can be used for encryption, by using the receiver public’s key (e,N) to encrypt our message, but also for signing, by using our own private key d for encryption. In this usage, we can prove that the message is ours by using our public key on the message.
Now that we have everything, let’s observe the RSA implementation in the binary.
First, we can spot the function that pick the two primes numbers p and q:
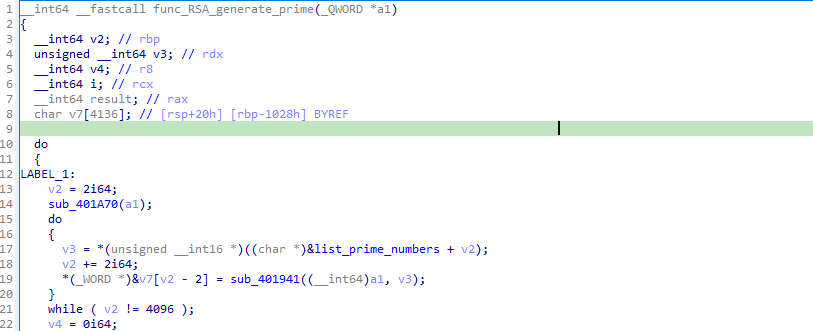
list_prime_numbers is actually a hardcoded list of the 250+ first prime numbers.
After having pand q, the two numbers are verified to see if they are not too close from each other (which would introduce a weakness). And after that, the modulus N is calculated:

Then, the private key d is generated, using (p-1)(q-1) (called phi)and the exponent e as a parameter:

Finally, a dummy encryption is done on some hardcoded values for whatever reason:
Going back to our main encryption function, we now have the labels for everything:
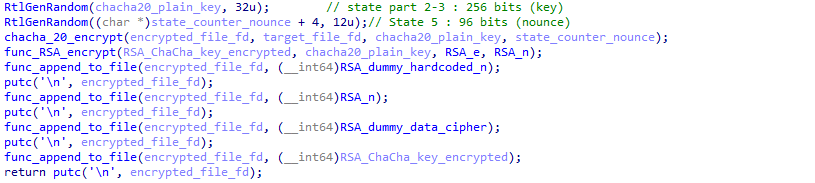
So basically, the xChaCha20 key is encrypted using the generated public key (e, N), and the modulus n is appended to the end of the encrypted file (the large hexadecimal number that we spot at first). The encrypted xChaCha20 key is also written in the file, along with two dummy values that we can ignore.
This is also a standard workflow, as RSA is a heavy algorithm to run. It’s common to see RSA being used as a mean to exchange a symetric-algorithm key, then a switch to symmetric encryption between the sender and the receiver.
The issue with this is that it is a perfectly standard and secure RSA implementation and usage. And since we cannot recover the private key d for the encrypted file we need to recover, we are stuck.
Or maybe not …
A small mistake with serious consequences
As we don’t have to (and can’t) break RSA to solve this challenge, we must have missed something.
After reviewing everything, we can spot that something very subtle is happening during the RSA key pair generation, and more precisely during the generation of the private key d:

RSA_e is set to 65537 before the call to func_RSA_generate_d, but during the function, it is overwritten by the value of d (as it is a hardcoded values passed by reference, we can easily miss it):

And this changes everything! Instead of using a perfectly secure public key (e, N) to encrypt the xChaCha20 secret key, the binary is using the private key d to encrypt the secret which is not using RSA for encryption anymore but … RSA for signing.
And since we have the modulus n (added at the end of the encrypted file) and the exponent e (hardcoded), we have the public key (e, N). And we can use this public key to ““decrypt”” (I know, it’s ugly to say that, but it technically is a non-secure form of decryption) the xChaCha20 key:
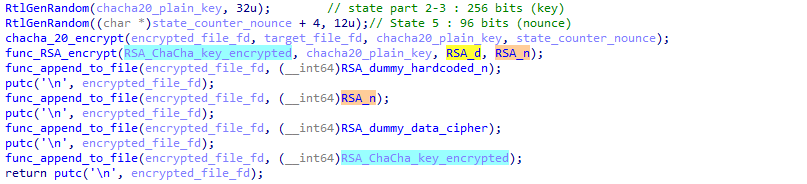
From that, we’ll be able to decrypt the file and hopefully retrieve its original content.
Scripting
Let’s script something to decrypt the file:
from Crypto.Cipher import ChaCha20
# Pub key decryption ¯\_(ツ)_/¯
def decrypt(ciphertext, e, n):
return int(pow(ciphertext, e, n))
with open("/tmp/SuspiciousFile.txt.Encrypted", "rb") as f:
content = f.read()
_chacha_cipher = content.split(b"9f1877")[0]
_cipher = str(content).split("\\n")[-2]
_n = str(content).split("\\n")[1]
e = 65537
n = int(_n, 16)
cipher = int(_cipher, 16)
print("n: %s\n" % str(n))
print("e: %s\n" % str(e))
print("encrypted: %s\n" % str(_cipher))
dec_re = decrypt(cipher, e, n)
print("rsa_decrypt(encrypted, e, n) : %s\n" % str(hex(dec_re)))
# ChaCha20 decrypt
tmp = "%x" % dec_re
_key = tmp[32:]
_nounce = tmp[0:24]
key = "".join(reversed([_key[i:i+2] for i in range(0, len(_key), 2)]))
nounce = "".join(reversed([_nounce[i:i+2] for i in range(0, len(_nounce), 2)]))
print("XChaCha20 key: %s\n" % str(key))
print("XChaCha20 nounce: %s\n" % str(nounce))
print("XChaCha20 encrypted: %s\n" % str(_chacha_cipher))
cipher = ChaCha20.new(
key=bytearray.fromhex(key),
nonce=bytearray.fromhex(nounce)
)
plaintext = cipher.decrypt(_chacha_cipher)
print("plaintext: %s" % plaintext)
We are basically retrieving the RSA public key component from the encrypted file, and using it against the “signed”/”encrypted” xChaCha20 key, also extracted from the file.
And finally, we can decrypt the raw file content using the retrieved key:
python3 solve.py
n: 154671286431635399459903186051766199603679670553099895666204249029447266966645858342970442270068233093984366394798156657457094358716995837385306200583522859131851729834717840285439348558248721066977314100080421961420613558242790821699248215344363345705466824979223515381488599140548711737932543441236986141641
e: 65537
encrypted: 5a04e95cd0e9bf0c8cdda2cbb0f50e7db8c89af791b4e88fd657237c1be4e6599bc4c80fd81bdb007e43743020a245d5f87df1c23c4d129b659f90ece2a5c22df1b60273741bf3694dd809d2c485030afdc6268431b2287c597239a8e922eb31174efcae47ea47104bc901cea0abb2cc9ef974d974f135ab1f4899946428184c
rsa_decrypt(encrypted, e, n) : 0x958f924dfe4033c80ffc490200000000989b32381e5715b4a89a87b150a5d528c943a775e7a2240542fc392aa197b001
XChaCha20 key: 01b097a12a39fc420524a2e775a743c928d5a550b1879aa8b415571e38329b98
XChaCha20 nounce: 0249fc0fc83340fe4d928f95
XChaCha20 encrypted: b'\x7f\x8a\xface\x9c^\xf6\x9e\xb9\xc3\xdc\x13\xe8\xb21:\x8f\xe3m\x94\x864!F+o\xe8\xad0\x8d*y\xe8\xea{f\t\xd8\xd0X\x02=\x97\x14k\xf2\xaa`\x85\x06HM\x97\x0eq\xea\x82\x065\xbaK\xfcQ\x8f\x06\xe4\xadi+\xe6%['
plaintext: b'Hello!\n\nThe flag is:\n\nR$A_$16n1n6_15_0pp0$17e_0f_3ncryp710n@flare-on.com\n'
A fun challenge that I really enjoyed, probably one of my favorite this year. Even if it turns me into a complete madman when I realized I was reversing an optimized RSA algorithm function for days without understanding anything, I still love this one.
R$A_$16n1n6_15_0pp0$17e_0f_3ncryp710n@flare-on.com

